⏶14
布尔巴基:用于定理证明的自生成和目标条件 MDP
发表
由  Haitham Bou Ammar 提交
Haitham Bou Ammar 提交
作者: Matthieu Zimmer, Xiaotong Ji, Rasul Tutunov, Anthony Bordg, Jun Wang, Haitham Bou Ammar
摘要
对于大型语言模型 (LLMs) 而言,推理仍然是一项具有挑战性的任务,尤其是在自动定理证明 (ATP) 的逻辑约束环境中,原因在于稀疏的奖励和证明的巨大规模。在 PutnamBench 等基准测试中,这些挑战会被放大,因为 PutnamBench 包含需要复杂的多步骤推理的大学水平问题。为了解决这个问题,我们引入了自生成目标条件 MDP (sG-MDP),这是一个新的框架,其中智能体根据不断发展的证明状态生成并追求其子目标。鉴于这种更结构化的目标生成方式,由此产生的问题更容易进行搜索。然后,我们将类似于蒙特卡洛树搜索 (MCTS) 的算法应用于解决 sG-MDP,并在 Bourbaki (7B) 中实例化我们的方法,Bourbaki (7B) 是一个模块化系统,可以集成多个 7B LLM 用于子目标生成和策略合成。在 PutnamBench 上,Bourbaki (7B) 解决了 26 个问题,以这种规模的模型实现了新的最先进的结果。
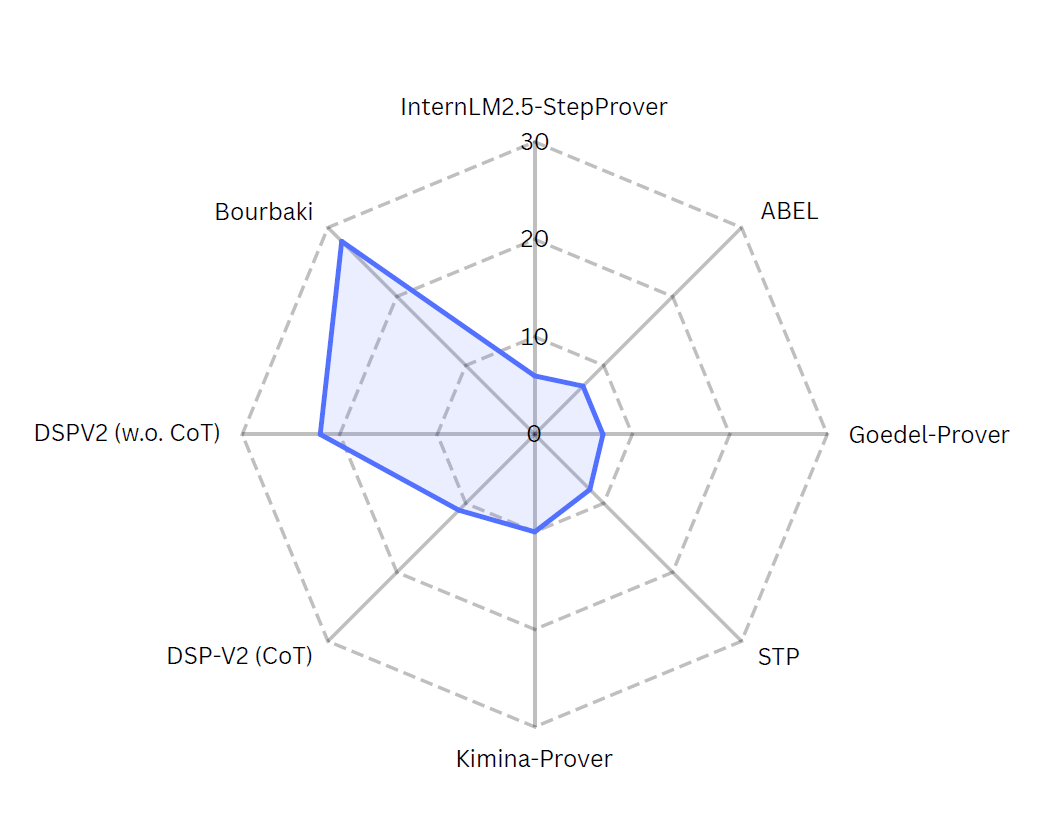
我们提出了一种用于自动定理证明的新算法,在 PutnamBench 上展示了最新的成果。我们将我们的方法称为 Bourbaki (7B),其灵感来自以严谨和系统化的数学方法而闻名的法国数学家假名团体;请查看他们 (https://en.wikipedia.org/wiki/Nicolas_Bourbaki) :=D